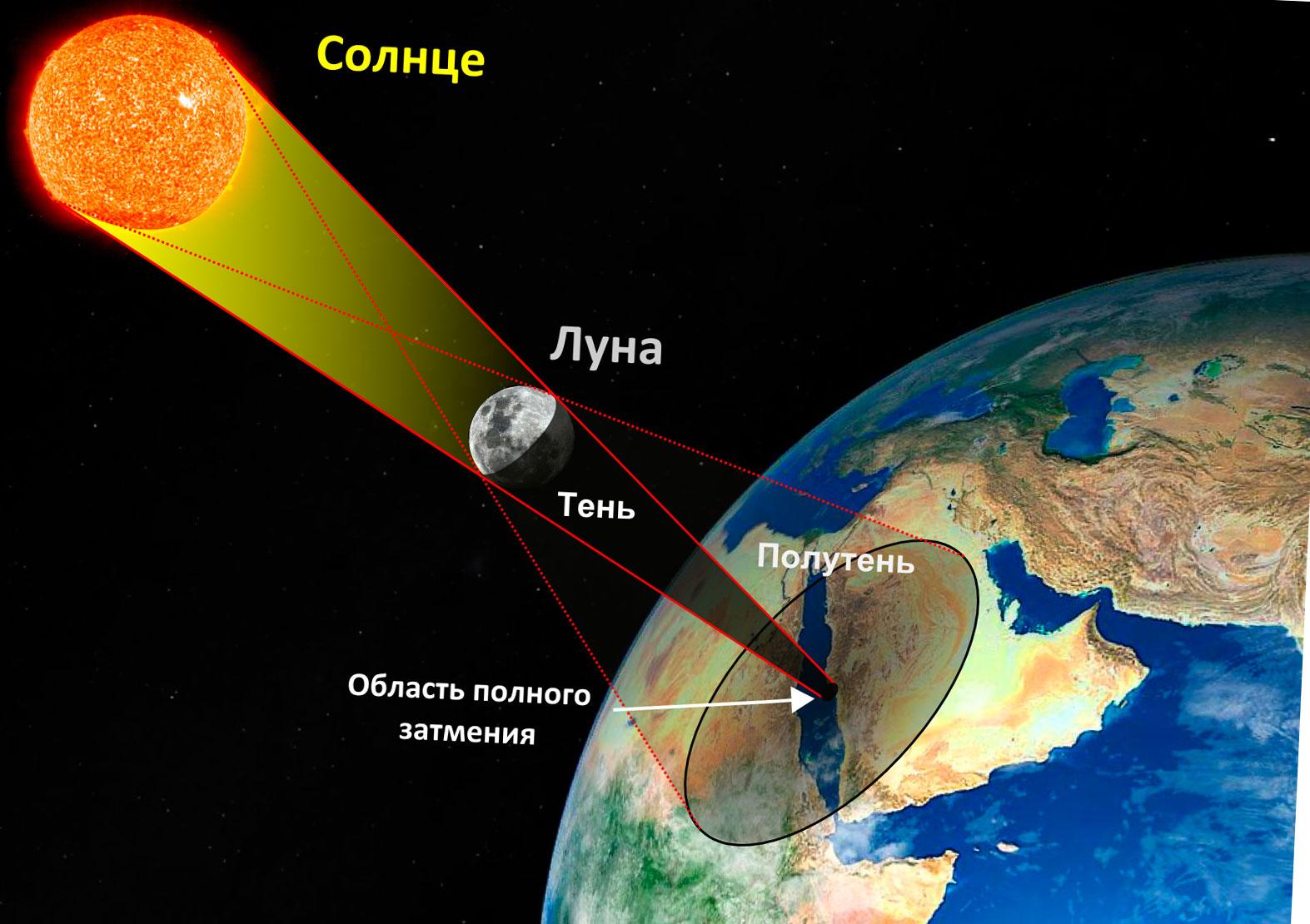
Gekleurde vierkante en sonsverduisterings

Die artikel beskryf my klasse vir middelskoolleerlinge – beurshouers van die Nasionale Kinderfonds. Die stigting soek veral begaafde kinders en jeugdiges (van graad XNUMX van laerskool tot hoërskool) en bied "beurse" aan geselekteerde studente. Hulle bestaan ​​egter glad nie uit die onttrekking van kontant nie, maar in omvattende sorg vir die ontwikkeling van talent, as 'n reël, oor baie jare. Anders as baie ander projekte van hierdie tipe, neem bekende wetenskaplikes, kultuurfigure, prominente humaniste en ander wyse mense, asook sommige politici, die Stigting se wyke ernstig op.

Die Stigting se aktiwiteite strek tot alle dissiplines wat basiese skoolvakke is, behalwe vir sport, insluitend kuns. Die fonds is in 1983 geskep as 'n teenmiddel teen die destydse werklikheid. Enigeen kan by die fonds aansoek doen (gewoonlik deur 'n skool, verkieslik voor die einde van die skooljaar), maar daar is natuurlik 'n sekere sif, 'n sekere kwalifikasieprosedure.

Soos ek reeds genoem het, is die artikel gebaseer op my meesterklasse, spesifiek in Gdynia, in Maart 2016, by die 24ste junior hoërskool by die III hoërskool. Vloot. Vir baie jare is hierdie seminare georganiseer onder die beskerming van die Stigting deur Wojciech Thomalczyk, 'n onderwyser van buitengewone charisma en hoë intellektuele vlak. In 2008 het hy die toptien in Pole betree, wat die titel van Professor in Pedagogiek (jare gelede deur die wet daarvoor voorsiening gemaak) bekroon is. Daar is 'n effense oordrywing in die stelling: "Onderwys is die as van die wêreld".

en die maan is altyd fassinerend - dan kan jy voel dat ons op 'n klein planeet in 'n groot ruimte woon, waar alles in beweging is, gemeet in sentimeters en sekondes. Dit maak my selfs 'n bietjie bang, ook die tydsperspektief. Ons leer dat die volgende algehele verduistering, sigbaar vanaf die gebied van vandag se Warskou, in ... 2681 sal wees. Ek wonder wie sal dit sien? Die oënskynlike groottes van die Son en Maan in ons lug is amper dieselfde – dis hoekom verduisterings so kort en so skouspelagtig is. Vir eeue behoort daardie kort minute genoeg te wees vir sterrekundiges om die sonkorona te sien. Dit is vreemd dat hulle twee keer per jaar gebeur... maar dit beteken net dat hulle iewers op Aarde vir 'n kort tydperk gesien kan word. As gevolg van getybewegings beweeg die Maan weg van die Aarde – oor 260 miljoen jaar sal dit so ver wees dat ons (ons???) net ringvormige verduisterings sal sien.

Blykbaar die eerste om te voorspel verduistering, was Thales van Milete (28-585 eeue vC). Ons sal waarskynlik nie weet of dit werklik gebeur het nie, dit wil sê of hy dit voorspel het, want die feit dat die verduistering in Klein-Asië plaasgevind het op Mei 567, 566 vC, is 'n feit wat deur moderne berekeninge bevestig word. Natuurlik haal ek data aan vir vandag se tydsberekening. Toe ek 'n kind was, het ek my voorgestel hoe mense jare getel het. So dit is byvoorbeeld XNUMX vC, Oujaarsaand kom en mense is bly: net XNUMX jaar vC! Hoe bly moes hulle tog gewees het toe “ons era” uiteindelik aangebreek het! Wat 'n millenniumwisseling het ons 'n paar jaar gelede beleef!

Die wiskunde van die berekening van datums en reekse verduisterings, is nie besonder ingewikkeld nie, maar is propvol allerhande faktore wat verband hou met reëlmaat en, nog erger, met die ongelyke beweging van die liggaam in wentelbane. Ek sou selfs graag hierdie wiskunde wou weet. Hoe kon Thales van Miletus die nodige berekeninge maak? Die antwoord is eenvoudig. Jy moet 'n lugkaart hê. Hoe om so 'n kaart te maak? Dit is ook nie moeilik nie, die antieke Egiptenare het geweet hoe om dit te doen. Om middernag kom twee priesters op die dak van die tempel uit. Elkeen van hulle gaan sit en teken wat hy sien (soos sy kollega). Na tweeduisend jaar weet ons alles oor die beweging van die planete ...

Pragtige geometrie, of pret op die "mat"

Die Grieke het nie van getalle gehou nie, hulle het hul toevlug tot meetkunde gebruik. Dit is wat ons sal doen. Ons verduistering hulle sal eenvoudig, kleurvol wees, maar net so interessant en eg. Ons aanvaar die konvensie dat die blou figuur so beweeg dat dit die rooi een verduister. Kom ons noem die blou figuur die maan, en die rooi figuur die son. Ons vra onsself die volgende vrae:

1. hoe lank duur 'n verduistering;
2. wanneer die helfte van die teiken gedek is;

   Rys. 1 Veelkleurige "tapyt" met die son en maan

3. wat die maksimum dekking is;
4. is dit moontlik om die afhanklikheid van die skilddekking betyds te ontleed? In hierdie artikel (ek word beperk deur die hoeveelheid teks) sal ek op die tweede vraag fokus. Hieragter is 'n mooi geometrie, miskien sonder vervelige berekeninge. Kom ons kyk na fig. 1. Kan dit aanvaar word dat dit geassosieer sal word met ... 'n sonsverduistering?

Ek moet eerlik sê dat die take wat ek gaan bespreek spesiaal gekies sal word, aangepas by die kennis en vaardighede van middel- en hoërskoolleerlinge. Maar ons oefen op sulke take soos musikante speel toonlere, en atlete doen algemene ontwikkelingsoefeninge. Buitendien, is dit nie net 'n pragtige mat (fig. 1) nie?

Rys. 2 "Blou" Maan en "Rooi" Son

Ons hemelliggame sal, ten minste aanvanklik, gekleurde vierkante wees. Die maan is blou, die son is rooi (die beste om in te kleur). met die hede verduistering Die maan jaag die son oor die lug, haal in ... en maak dit toe. Dit sal dieselfde wees met ons. Die eenvoudigste geval, wanneer die Maan relatief tot die Son beweeg, soos in Fig. 2. 'n Verduistering begin wanneer die rand van die Maan se skyf die rand van die Son se skyf raak (Fig. 2) en eindig wanneer dit verby dit gaan.

Rys. 3 Die maan nader die son skuins

Ons neem aan dat die "Maan" een sel per tydeenheid beweeg, byvoorbeeld per minuut. Die verduistering duur dan agt eenhede van tyd, sê minute. Die helfte sonsverduisterings heeltemal verdof Die helfte van die draaiknop word twee keer gesluit: na 2 en 6 minute. Die persentasie verduistering grafiek is eenvoudig. Gedurende die eerste twee minute sluit die skild eweredig teen 'n tempo van nul tot 1, die volgende twee minute word dit teen dieselfde tempo blootgestel.

Hier is 'n meer interessante voorbeeld (Fig. 3). Die maan nader die son skuins. Volgens ons per-minuut-betalingsooreenkoms duur die verduistering 8√2 minute - in die middel van hierdie tyd het ons 'n totale verduistering. Kom ons bereken watter deel van die son bedek is na tyd t (Fig. 3). As t minute verloop het sedert die begin van die verduistering, en as gevolg daarvan is die Maan soos in Fig. 5, dan (aandag!) Daarom is dit bedek (die oppervlakte van die vierkantige APQR), gelyk aan die helfte van die sonskyf; daarom is dit bedek wanneer, d.w.s. na 4 minute (dan 4 minute voor die einde van die verduistering).

Rys. 4 Grafiek van die "shading"-funksie

Totaliteit duur een oomblik (t = 4√2), en die grafiek van die "geskakeerde deel"-funksie bestaan ​​uit twee boë parabole (Fig. 4).

Ons blou maan sal die hoek met die rooi son raak, maar dit sal dit bedek, nie skuins nie, maar effens skuins.Interessante meetkunde verskyn wanneer ons die beweging 'n bietjie kompliseer (Fig. 6). Die rigting van beweging is nou vektor [4,3], dit wil sê, "vier selle na regs, drie selle op." Die posisie van die Son is sodanig dat die verduistering begin (posisie A) wanneer die sye van die "hemelliggame" tot 'n kwart van hul lengte konvergeer. Wanneer die Maan na posisie B beweeg, sal dit een sesde van die Son verduister, en in posisie C sal dit die helfte verduister. In posisie D het ons 'n totale verduistering, en dan gaan alles terug, "soos dit was."

Rys. 5 Deel van die Son versteek gedurende tyd t

Die verduistering eindig wanneer die Maan in posisie G is. Dit het so lank geduur as seksie lengte AG. As ons, soos voorheen, as 'n eenheid van tyd die tyd neem waartydens die Maan "een vierkant" verbygaan, dan is die lengte van die AG gelyk. As ons teruggaan na die ou konvensie dat ons hemelliggame 4 by 4 is, sou die resultaat anders wees (wat?). Soos dit maklik is om te wys, sluit die teiken na t < 15. Die grafiek van die “persentasie van skermdekking”-funksie kan in fig. 6.

Rys. 6 Grafiek van die "persent beskerming" funksie

Verduistering en sprongvergelyking

Rys. 7 Obstruksie van die sonskyf tydens die verduistering wat in fig. 6

Die probleem van verduisterings sou onvolledig wees as ons nie die geval van sirkels in ag neem nie. Dit is baie meer ingewikkeld, maar kom ons probeer uitvind wanneer een sirkel die helfte van die ander verduister - en in die eenvoudigste geval, wanneer een van hulle langs die deursnee beweeg wat hulle albei verbind. Die tekening is bekend aan die houers van een of ander kredietkaart.

Die berekening van die posisie van die velde is ingewikkeld, aangesien dit eerstens kennis van die formule vir die oppervlakte van 'n sirkelvormige segment vereis, tweedens kennis van die boog van die hoek, en derdens (en die ergste van alles), die vermoë om 'n sekere sprongvergelyking op te los. Ek sal nie verduidelik wat 'n "oorgangsvergelyking" is nie, kom ons kyk na 'n voorbeeld (Fig. 8).

Rys. 8 "Sferiese" verduistering

'n Sirkelvormige snit is die "bak" wat oorbly nadat 'n sirkel met 'n reguit lyn gesny is. Die oppervlakte van so 'n segment is S = 1/2r²(φ-sinφ), waar r die radius van die sirkel is, en φ die sentrale hoek is waarop die segment rus (Fig. 8). Dit word maklik verkry deur die oppervlakte van die driehoek van die oppervlakte van die sirkelsektor af te trek.

Episode O₁O₂ (die afstand tussen die middelpunte van die sirkels) is dan gelyk aan 2rcosφ/2, en die hoogte (breedte, "middellyn") h = 2rsinφ/2. Dus, as ons wil bereken wanneer die Maan die helfte van die sonskyf sal bedek, moet ons die vergelyking oplos: wat, na vereenvoudiging, word:

Rys. 9 Grafieke van twee funksies

Die oplossing van sulke vergelykings is buite die bestek van eenvoudige algebra - die vergelyking bevat beide hoeke en hul trigonometriese funksies. Die vergelyking is buite die bereik van tradisionele metodes. Dis hoekom dit genoem word om te spring. Kom ons kyk eers na die grafieke van beide funksies, dit wil sê funksies en funksies. Ons kan 'n benaderde oplossing uit hierdie figuur lees. Ons kan egter 'n iteratiewe benadering kry of ... gebruik die Oplosser-opsie in die Excel-sigblad. Elke hoërskoolleerling behoort dit te kan doen, want dit is die 20ste eeu. Ek het 'n meer gesofistikeerde Mathematica-instrument gebruik en hier is ons oplossing met XNUMX desimale plekke van onnodige akkuraatheid:

StelPresisie[VindRoot[x==Sin[x]+Pi/2,{x,2}],20] {x⇒2.3098814600100574523}.

Rys. 10 Animasie van verduistering in matematica

Ons verander dit in grade deur met 180/π te vermenigvuldig. Ons kry 132 grade, 20 minute, 45 en 'n kwart van 'n boogsekonde. Ons bereken dat die afstand na die middel van die sirkel O is₁O₂ = 0,808 radius, en "middellyf" 2,310.